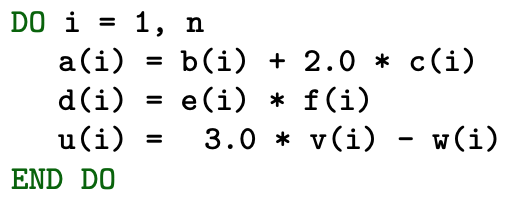Scalar optimization
Scalar optimization consists of improving the usage of the ressources used by your application on the node it’s running on (cpu, memory and disk) to reduce the execution time. One can work a posteriori with profiling tools but one can apply some optimization strategies during the writing of the source files. Some advices are given below to help you.
1. Memory
The way memory is traversed has a great importance because of time lost waiting for data that are not present if your application requests data that are dispersed in the memory and not stored contiguously.
1.2. Cache memory
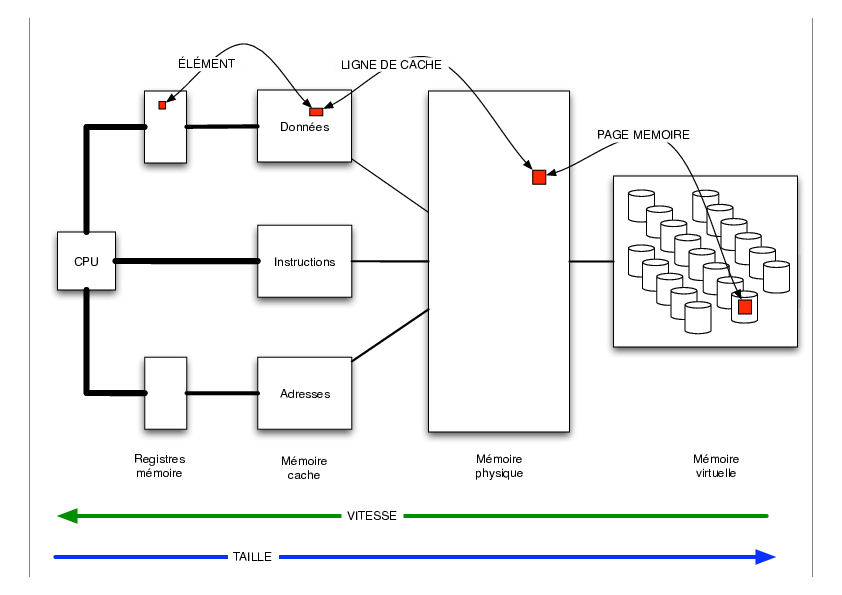
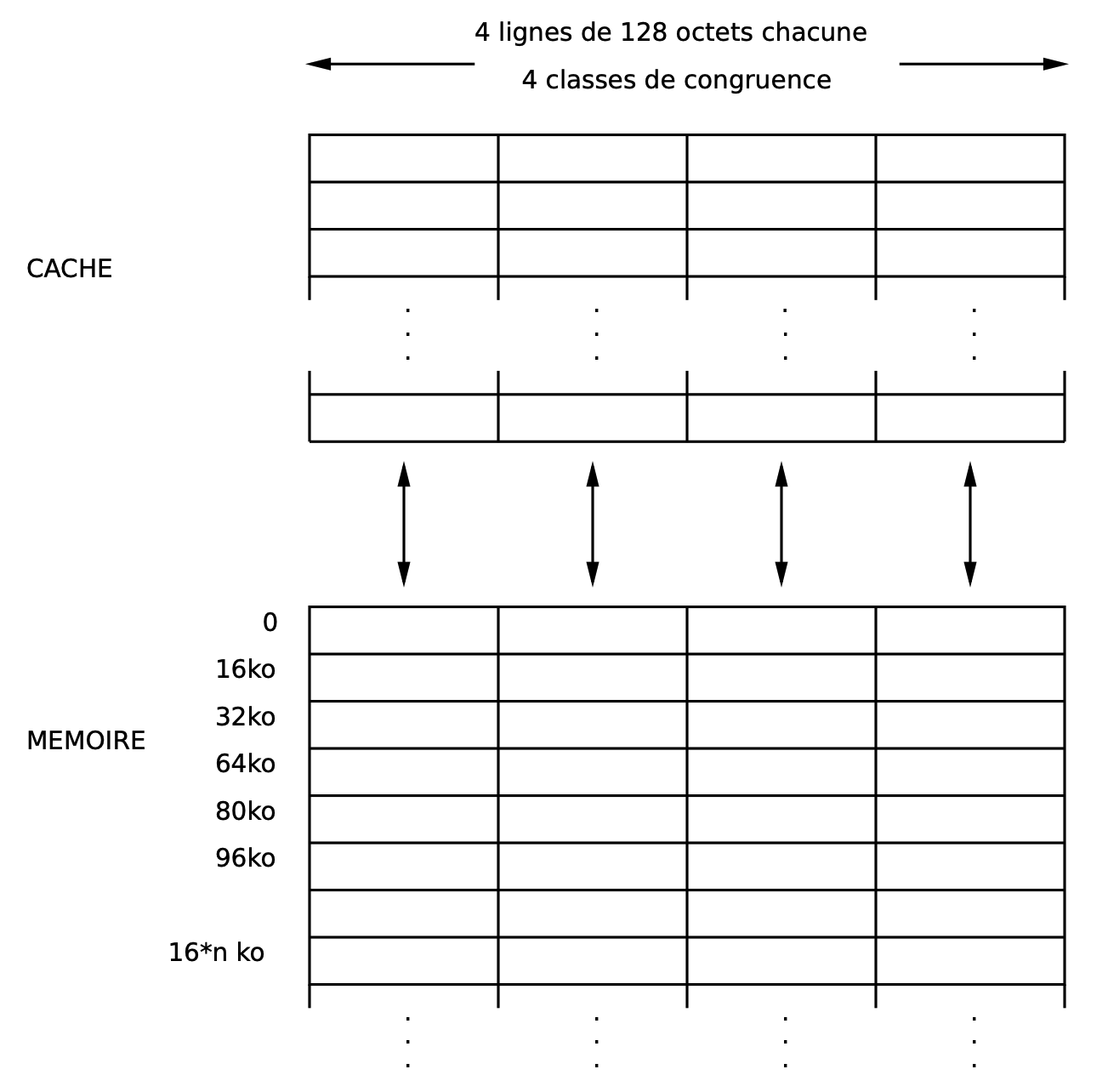
The memory cache is a memory, on the chip, that is very small but very fast. Its goal is to keep data near the processor such that they are rapidly accessed. The memory cache is a set of several ways, that have addresses like the main memory.
When a data is requested by the CPU, there are two possibilities :
-
if it’s not present in the cache, it comes from the main memory, it goes through the cache hierarchy, and it is stored in the cache. The address in the cache memory is computed as the remainder of an integer division (the global address divided by the size of the cache way). The way in which the data is stored depends on a policy applied on the managing of the cache ways (for example least recently used). Looking for the data in the main memory slows down the execution of the application.
-
if it’s already present, it’s directly used, some time is gained !
When a data is requested from memory, in fact, a cache line is brought back from memory, so several values for the cost of only one. So one should use them !
When a program looks for a data, another structure is used : the TLB (Table Lookaside Buffer) whose entries are references to memory pages, i.e. the way to reach them on the hardware of the node. It works like a cache memory but for memory pages. So if your application goes through memory in all directions the TLB is refreshed too often and new entries have to be computed all the time. This consumes a lot of time too and your application has to wait for it.
So some advices could be :
-
minimize the cache misses : use data already in the cache as much as possible → reuse data !
-
minimize the TLB misses : travel linearly through the memory
2. Arrays
Arrays are very important in HPC because scientific problems have lots of data to store, most of them are of the same nature, so arrays of integers or floats (for example) are widely used. To better represent the problem addressed, one has the possibility to use multi-dimensional arrays (like in Fortran). One important thing is to understand how those arrays are stored in memory and how to walk through them.
Let’s take a 2D array like this one :
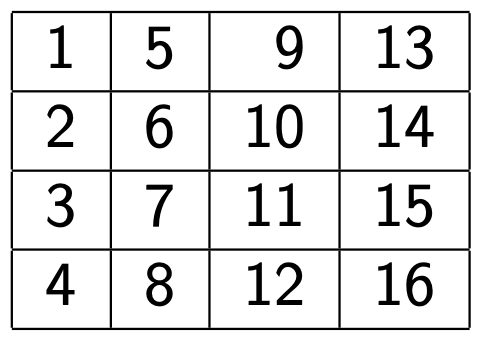
This 2D array is stored like this in Fortran :
So it is stored following columns and not lines (like in C/C++).
One calls stride the step between two consecutively addressed elements of an array. One should try to have as often as possible a stride of 1. If your stride is bigger, even very large, you loose the gain of the other elements brought back within the same cache line : they are wiped away before been used.
2.1. Browse a table
As mentioned above, the best way to browse an array is to follow its storage in memory. In case of a multidimensional array, it’s the same, and one should iterate over it with nested loops correctly nested
2.2. Ways of accessing elements of an array
There are different ways to access the elements of an array in a loop, when going through an array. Some are better than others. Here are some Fortran examples :
Loop indexes should be declared as integer variables.
Some remarks :
-
The best way is the more to the left example : one keeps the multidimensional structure of the array, and we have two embedded loops
-
Having a multidimensional array stored like an 1D array is not bad, but it costs a little to compute the index ; maybe a single loop is better if possible
-
A bad example because the compiler has lost the link between the loop indexes and the course in the table : no optimization like unrolling, vectorization are possible
-
The worse case : indirect access to the array elements : it’s only known at runtime
3. Floating point values precision
Floating point variables can be badly initialized and useful information is lost from the early stages. So one has to be careful when handling numerical constants.
These Fortran examples show how forgetting the kind (simple or double) of numerical constants can produce erroneous results
4. Operation optimization
All operation have a cost but some cost more than others. For example, the floating point division is expensive and in some cases (division of a lot of numbers by the same value) it may be replaced by the multiplication of the reciprocal.
5. Boundary condition treatment
In physical problems one has to handle the first and last points of a direction on a mesh. The bad idea is to keep them in the loop and to test the value of the loop index.
It’s better to remove the tests from the loop, because tests inhibit optimizations in loops.
Vectorization
Vectorization is about doing the same operation on multiple data. In general one calls it a SIMD : Single Instruction Multiple Data
There are some conditions to be enabled to vectorize (there are some exceptions) :
-
loops with real indexes, and known bounds
-
if nested, only the most inner loop can be vectorized
-
there should be "independence" between iterations
-
no test
-
no function calls
1. Principles
1.1. Small loop
Here is a simple loop
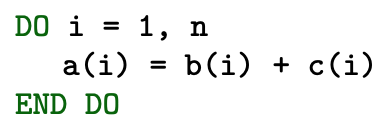
The execution in scalar mode can be mimic like this :
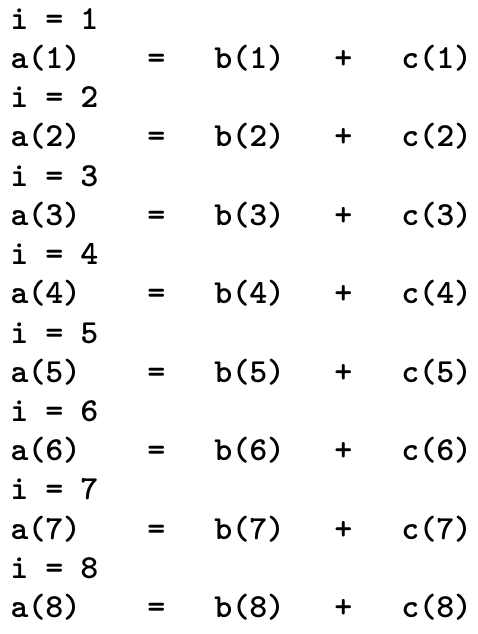
As there is no dependence, one can vectorize this loop and the execution looks like :
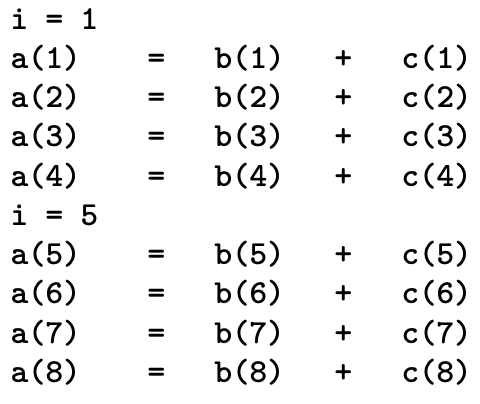
With the vectorization, one can see that instructions are treated by groups. The length of vector registers decides the number of iterations treated together. Vector registers become longer as technology (AVX, AVX2, AVX512, …) improves.
2. Dependencies
A classification of some kinds of dependencies has been proposed (CAC Cornwell University)
2.1. Read After Write (RAW)
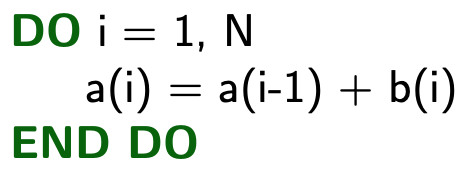
Known as "flow dependency". The variable is written and then read.
→ Not Vectorizable
2.2. Write After Read (WAR)
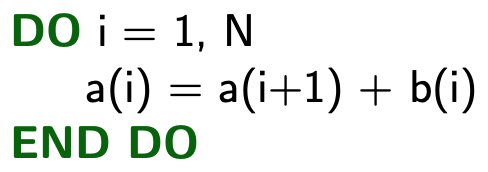
Known as "flow dependency". The variable is read and then written.
→ Vectorizable
2.3. Read After Read (RAR)
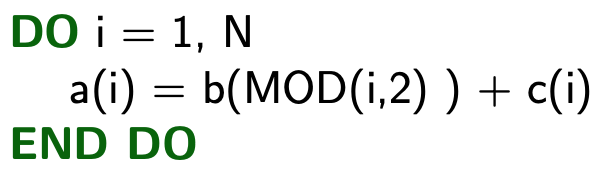
Not really a dependency. The variable is read and then read again.
→ Vectorizable
2.4. Write After Write (RAW)
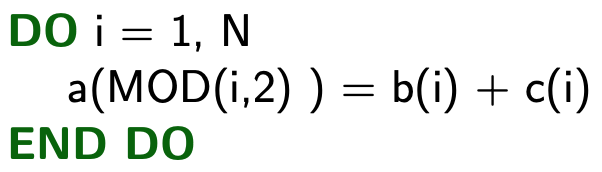
Known as "flow dependency". The variable is written and then written again.
→ Not Vectorizable
2.5. Aliasing
Aliasing appears when two identifiers point to memory areas that intersect. That may be a problem for correct vectorization. In C programming, one can use the keyword restrict at the function declaration to specify that it doesn’t occur for its arguments.
2.6. Calling function
Calling function inhibits vectorization. Some calls can be handled by the compiler and the vectorization is possible when the function is small and the compiler has access to its content (inlining).
Standard mathematical functions are vectorizable.
In Fortran, calls to functions that have the ELEMENTAL keyword can be vectorized.
3. Implementation
If the compiler uses at least the -O3 optimization level, the vectorization is enabled.
Each compiler has its own flags.
3.1. Flags for Intel compilers
One can use the following flags to activate vectorization on resp. AVX, AVX2, AVX512 : -xAVX, -xCORE-AVX2, -xCORE-AVX512 .
For getting full support of AVX512, one should add the following option -qopt-zmm-usage=high .
To get some diagnostics on how the vectorization is done by the compiler, one can add the following options to get some reports : -qopt-report=5 -qopt-report-phase=vec .
The following options inhibit vectorization : -no-vec -no-simd -qno-openmp-simd .
3.2. Flags for GNU compilers
The vectorization is activated by the option -ftree-vectorize (added by default at -O3 level).
One can use the following flags to activate vectorization on resp. AVX, AVX2, AVX512 : -mavx, -mavx2, -mavx512f -mavx512dq -mavx512bw -mavx512vbmi -mavx512vbmi2 -mavx512vl .
To get some diagnostics on how the vectorization is done by the compiler, one can add the following option to get some reports : -fopt-info-vec-all .
The following option inhibits vectorization : -fno-tree-vectorize .